Thế Nào Là Tỉ Lệ Thuận? Các Nguyên Lý Cơ Bản

Trong bài viết dưới đây, Phương Pháp Việt sẽ chia sẻ lý thuyết về đại lượng tỉ lệ thuận, bao gồm thế nào là tỉ lệ thuận, các tính chất cơ bản và các loại tỉ lệ thuận trong toán học. Điều này giúp học sinh có thể hiểu rõ hơn về chủ đề này và áp dụng kiến thức vào việc giải các bài tập tương ứng.

Thế nào là tỉ lệ thuận?

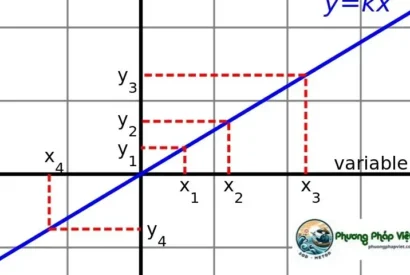
Định nghĩa về đại lượng tỉ lệ thuận là khi một đại lượng y phụ thuộc vào một đại lượng x theo một công thức cụ thể: y = kx (với k là một hằng số khác không), chúng ta nói rằng y tỉ lệ thuận với x với hệ số tỉ lệ k.

Bạn đang xem Thế Nào Là Tỉ Lệ Thuận? Các Nguyên Lý Cơ Bản tại chuyên mục Giải đáp của website Phương Pháp Việt

Cần lưu ý rằng khi y tỉ lệ thuận với x theo hệ số tỉ lệ k (khác không), thì x cũng tỉ lệ thuận với y theo hệ số tỉ lệ 1/k. Ta nói rằng hai đại lượng đó có tỷ lệ thuận với nhau.

Ví dụ: Nếu y = 4x, thì y tỉ lệ thuận với x với hệ số 4, và tương tự, x tỉ lệ thuận với y với hệ số 1/4.

Các tính chất của đại lượng tỉ lệ thuận:

• Nếu hai đại lượng tỉ lệ thuận với nhau, tỉ số của hai giá trị tương ứng luôn không đổi.
• Tỉ số của bất kỳ hai giá trị nào của hai đại lượng này cũng bằng tỉ số của hai giá trị tương ứng của đại lượng kia.
• Nếu hai đại lượng y và x tỉ lệ thuận với nhau theo tỉ số k, thì ta có công thức y = kx.
• 

Công thức tính đại lượng tỉ lệ thuận

Hai đại lượng x và y tỉ lệ thuận với nhau nếu chúng liên hệ theo công thức y = kx, với k là một hằng số khác không. Khi đó, chúng ta nói rằng y tỉ lệ thuận với x theo hệ số tỉ lệ k.

Tỉ lệ thuận trực tiếp

Tỉ lệ thuận trực tiếp là một khái niệm toán học mô tả mối quan hệ giữa hai biến trong đó khi một biến tăng, biến còn lại cũng tăng theo cùng một tỷ lệ. Để tính toán tỉ lệ thuận trực tiếp, sử dụng công thức Y = kX, trong đó Y là giá trị của biến phụ thuộc, X là giá trị của biến độc lập, và k chính là một hằng số tỉ lệ.

Ví dụ, nếu số tiền phải trả cho một sản phẩm tỉ lệ thuận trực tiếp với số lượng sản phẩm, ta có thể biểu diễn mối quan hệ này bằng công thức Y = 10X, trong đó X là số lượng sản phẩm và Y là số tiền phải trả. Khi số lượng sản phẩm tăng lên thành 10, số tiền phải trả cũng tăng lên thành 100 đồng.

Tỉ lệ thuận trực tiếp được áp dụng rộng rãi trong nhiều lĩnh vực như kinh tế, khoa học, xã hội và thống kê. Hiểu và áp dụng chính xác khái niệm này giúp chúng ta hiểu và nắm rõ hơn về mối quan hệ giữa các biến và qua đó có thể dự đoán được sự biến đổi của chúng trong các tình huống thực tế.

Tỉ lệ thuận nghịch biến

Tỉ lệ thuận nghịch biến là một khái niệm trong toán học miêu tả mối quan hệ giữa hai biến trong đó khi một biến tăng, biến còn lại thì giảm theo tỉ lệ ngược lại. Trong phần này, chúng ta sẽ tìm hiểu về tính chất, cách tính và xem xét một số ví dụ minh họa của tỉ lệ thuận nghịch biến.

Tính chất của tỉ lệ thuận nghịch biến:

• Khi một biến tăng, biến còn lại giảm theo tỉ lệ ngược lại. Điều này có nghĩa là nếu ta tăng giá trị của một biến lên, giá trị của biến còn lại sẽ giảm đi theo tỉ lệ ngược đó.
• Đồ thị của một tỉ lệ thuận nghịch biến thường là một đường cong nằm trong hệ trục tọa độ, thể hiện mối quan hệ ngược đó.

Cách tính tỉ lệ thuận nghịch biến:

• Để tính tỉ lệ thuận nghịch biến giữa hai biến, ta chia giá trị của biến thứ nhất cho giá trị của biến thứ hai. Kết quả sẽ cho ta một con số, gọi là hệ số tỉ lệ thuận nghịch biến.
• Hệ số tỉ lệ thuận nghịch biến thường được ký hiệu k và có thể có giá trị âm, hoặc dương hoặc bằng không. Giá trị dương của k thể hiện mối quan hệ nghịch biến giữa hai biến, trong khi giá trị âm của k thể hiện mối quan hệ thuận biến.

Ví dụ minh họa:

• Trong một bài toán về tốc độ và thời gian, nếu tốc độ tăng lên, thì thời gian cần để đi qua một quãng đường cụ thể sẽ giảm theo tỉ lệ thuận nghịch biến. Ví dụ, nếu tốc độ tăng gấp đôi, thì thời gian cần để đi qua quãng đường sẽ giảm một nửa.
• Một ví dụ khác là mối quan hệ giữa số công nhân và thời gian hoàn thành một công việc. Nếu số công nhân tăng lên, thì thời gian hoàn thành công việc sẽ giảm theo tỉ lệ thuận nghịch biến. Ví dụ, nếu số công nhân tăng gấp đôi, thì thời gian hoàn thành công việc sẽ giảm một nửa.

Kết luận

Hy vọng bãn đã hiểu được thế nào là tỉ lệ thuận. Tỉ lệ thuận không chỉ giúp chúng ta hiểu rõ mối quan hệ giữa các yếu tố trong các tình huống thực tế mà còn cho phép chúng ta dự đoán và tính toán các kết quả cụ thể.

Việc áp dụng tỉ lệ thuận không chỉ đơn giản là một công cụ tính toán mà còn là một phương tiện quý giá để tối ưu hóa quy trình kinh doanh và ra quyết định một cách thông minh và hiệu quả.