
Compound Annual Growth Rate (CAGR)
How to Calculate CAGR
The compound annual growth rate (CAGR) is the rate of return required for the value of an investment or financial metric to grow from its beginning value to its ending value between two dates.
In simple terms, the CAGR answers the question, “At what growth rate must the metric grow at each [Period] to reach [Ending Value] from [Beginning Value] under the time frame of [Number of Periods]?”
The CAGR is the rate of return of an investment—or a financial metric like revenue—across a predefined period, expressed in terms of an annual percentage.
CAGR measures growth as if the underlying investment or metric had grown at a fixed rate while compounding on an annual basis.
Therefore, CAGR is an estimate of the rate of return per year based on the pattern of growth in historical periods.
The step-by-step process to calculate CAGR is as follows.
- Step 1 Divide the Ending Value (or Future Value) by the Beginning Value (or Present Value)
- Step 2 Raise the Resulting Figure to the Inverse of the Number of Compounding Periods (1 ÷ t)
- Step 3 Subtract by One to Convert the Implied CAGR into Percent Form
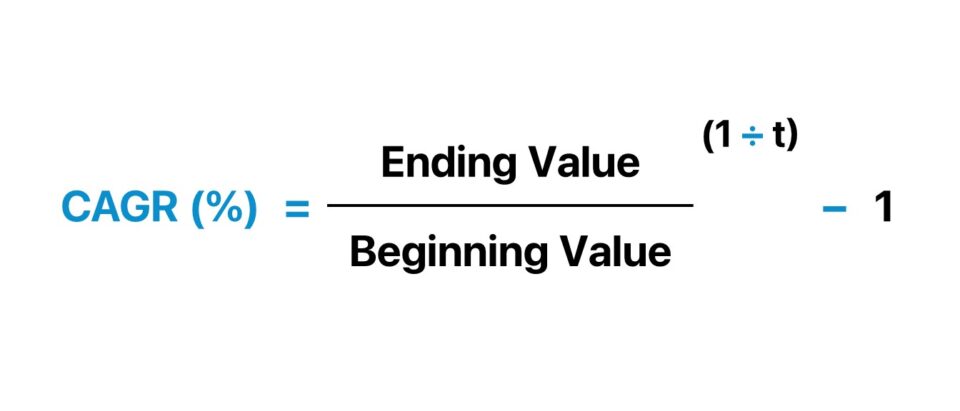
CAGR Formula
The compound annual growth rate (CAGR) formula is the ending value divided by the beginning value, raised to one divided by the number of compounding periods, and subtracts by one.
Where:
- Ending Value (or Future Value) The value at the end of the period (EoP).
- Beginning Value (or Present Value) The value at the beginning of the period (BoP).
- Number of Periods (t) The total number of compounding periods.
Or, the CAGR formula can also be expressed more formally using other financial terms.
The formula to calculate CAGR divides the future value (FV) by the present value (PV), raises the figure to one divided by the number of compounding periods, and subtracts by one.
Note: The difference between the CAGR formulas is merely the usage of financial jargon in the latter.
CAGR Calculation Example
Suppose there is a company with revenue of $20 million at the end of the current period (Year 0).
Five years from the present date, the company’s revenue is projected to reach $32.5 million (Year 5).
Given those assumptions, we’ll enter the following figures into the CAGR formula:
- Beginning Value (Present Value) = $20 million
- Ending Value (Future Value) = $32.5 million
- Number of Periods = 5 Years
In the first part of the formula, the ending value of $32.5 million is divided by the starting value of $20 million.
The resulting figure must then be annualized by raising it to the power of 1 divided by the 5 periods.
Lastly, once we subtract 1 from the return value, we are left with a CAGR of 10.2%.
- Compound Annual Growth Rate (CAGR) = ($32.5 million ÷ $20.0 million)^ (1 ÷ 5 Periods) - 1
- CAGR (%) = 10.2%
Year 0 is excluded when counting the number of periods, because only the periods when the revenue is compounding must be counted.
Hence, the beginning period number is subtracted from the ending period number (i.e. Year 5 minus Year 0 = 5 Years).
How to Use CAGR to Forecast
One of the more practical use cases of the compound annual growth rate (CAGR), aside from understanding historical growth, pertains to forecasting.
- Historical CAGR Analysis Once the historical CAGR has been computed, the figure can be referenced to establish the operating assumptions that drive a forecast model.
- “Sanity Check” of Forecast Model The historical CAGR should exceed the projected CAGR in most cases, albeit there are often exceptions. Thus, the implied CAGR from the forecast period (i.e. forward-basis) can be compared to the historical CAGR (i.e. backward looking) to confirm the operating assumptions are reasonable. If not, adjustments to the assumptions might be necessary.
- Forecast Using CAGR The CAGR metric can also be used to directly forecast the future value (FV) of an asset, which we will elaborate upon shortly.
The future value (FV) of an asset can be forecasted using the following formula, wherein CAGR is an input.
For example, suppose an investment portfolio is worth $10 million at the moment, with a historical CAGR of 5.0% across the trailing five years.
Based on historical financial data, the CAGR of the investment is projected to be 3.0% across the next five years.
- Present Value (PV) = $10 million
- Historical CAGR, Trailing Five-Year Period = 5.0%
- Forecast CAGR Assumption, Forward Five-Year Period = 3.0%
- Number of Compounding Periods (t) = 5 Years
Given the 3.0% CAGR assumption, the value of the investment portfolio at the end of Year 5 should reach approximately $12 million.
- Future Value (FV), Year 5 = $10 million × (1 + 3%)^5 = $12 million
What is the Conceptual Meaning of CAGR?
The compound annual growth rate (CAGR) is a practical metric to facilitate sound decision-making, but it is critical to understand that the CAGR as a standalone metric still does not reveal the entire story.
To truly grasp the conceptual meaning of CAGR, it is necessary to comprehend the benefits, as well as the metric’s limitations.
Benefits of CAGR
- Removal of Fluctuations → Since annualized growth metrics remove the fluctuations of year-over-year (YoY) growth rates, the single percent rate facilitates comparisons of CAGR over time between two companies or investments, which would otherwise be challenging to compare.
- “Sanity Check” → Since the CAGR metric can confirm whether the projections align with the industry average and historical growth, the CAGR metric can also be useful as a “sanity check”, i.e. to confirm the assumptions are reasonable.
- Convenience → The relative ease at which the CAGR can be computed is a notable benefit to using the metric, while still providing valuable insights into the growth profile of anything that rises (or falls) in value.
Limitations of CAGR
- Volatility Risk → One drawback to the CAGR is that the metric neglects the volatility associated with the underlying asset. The growth rate can therefore be misleading in the absence of year-over-year (YoY) data. For instance, a company’s revenue growth could be inflated if the positive growth is front-ended in the earlier periods before tapering off.
- Operating Drivers → Annualized metrics such as the CAGR should not be taken at face value to minimize the risk of understating (or overstating) the growth potential without understanding the underlying operating drivers.
- Historical Performance (≠) Future Performance → Per usual, “past performance is no guarantee of future results”. Therefore, relying on the historical CAGR to build a pro forma forecast requires a certain degree of caution. The historical CAGR (or industry averages) should serve as a precedent to reference, as part of a more in-depth analysis of the company (or investment).
Link nội dung: https://study-japan.edu.vn/compound-annual-growth-rate-cagr-a13474.html